Constant pH Molecular Dynamics Simulations

Figure 1: This titration curve of the tripeptide Asp-Glu-Asp is obtained by performing constant pH MD simulations in explicit solvent at different pH values. — **Figure 1**: This titration curve of the tripeptide Asp-Glu-Asp is obtained by performing constant pH MD simulations in explicit solvent at different pH values.

© MPI-NAT

**Figure 1**: This titration curve of the tripeptide Asp-Glu-Asp is obtained by performing constant pH MD simulations in explicit solvent at different pH values.

© MPI-NAT

Figure 2: Scheme of the three protonation states of Glu/Asp and His. The titrating reaction coordinate (λ1) is depicted with black arrows and the switching one (λ2) with red arrows. — **Figure 2**: Scheme of the three protonation states of Glu/Asp and His. The titrating reaction coordinate (λ₁) is depicted with black arrows and the switching one (λ₂) with red arrows.

© MPI-NAT, P. Dobrev

**Figure 2**: Scheme of the three protonation states of Glu/Asp and His. The titrating reaction coordinate (λ₁) is depicted with black arrows and the switching one (λ₂) with red arrows.

© MPI-NAT, P. Dobrev

Typically, in a molecular dynamics (MD) simulation, the protonation states of ionizable groups of a protein are set at the beginning of the simulation. This presetting is not always an obvious task, in particular for histidine, as its pK_a is close to the physiological pH. In contrast, in a constant pH MD simulation, the protonation state of an ionizable group of a protein is allowed to change during the simulation according to the local electrostatic environment and the actual pH of the solution.

In this model, the protonation state of an amino acid changes continuously by propagating the motion of a virtual particle (usually referred to as “λ-particle”) that interpolates between different protonation Hamiltonians in explicit solvent MD simulations. The pK_a values of the ionizable groups can then be obtained from the distributions of the protonation states.

The Three State Model

Amino acids such as aspartate (Asp), glutamate (Glu), or histidine (His) have two atoms that can carry a proton: two oxygen atoms for Asp and Glu and two nitrogen atom for His, respectively. To ensure correct representation of such residues, we developed a “three state model” that includes two protonated and one deprotonated form for Asp and Glu and one protonated and two deprotonated forms for His, respectively (Dobrev et al. 2016).

Validation

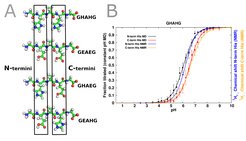
Our approach to calculate the protonation states has been tested in a recent study using challanging control pentapeptide systems. In comparison with results from NMR titration experiments, our method is suitable to not only reproduce the correct pK_a values in those systems but also to determine the direction of the shift from their reference values in solution (Dobrev et al. 2020).

Figure 3: A Illustration of the four pentapetide test systems: Gly-His-Asp-His-Gly, Gly-Glu-Asp-Glu-Gly, Gly-His-Asp-Glu-Gly, and Gly-Glu-Asp-His-Gly. The titrated residues are highlighted in the box. B Comparison of theoretical and experimental titration curves for the Gly-His-Asp-His-Gly peptide obtained in silico (black and red) and in NMR experiments (blue and orange). — **Figure 3**: A Illustration of the four pentapetide test systems: Gly-His-Asp-His-Gly, Gly-Glu-Asp-Glu-Gly, Gly-His-Asp-Glu-Gly, and Gly-Glu-Asp-His-Gly. The titrated residues are highlighted in the box. B Comparison of theoretical and experimental titration curves for the Gly-His-Asp-His-Gly peptide obtained *in silico* (black and red) and in NMR experiments (blue and orange).

© MPI-NAT, P. Dobrev

**Figure 3**: A Illustration of the four pentapetide test systems: Gly-His-Asp-His-Gly, Gly-Glu-Asp-Glu-Gly, Gly-His-Asp-Glu-Gly, and Gly-Glu-Asp-His-Gly. The titrated residues are highlighted in the box. B Comparison of theoretical and experimental titration curves for the Gly-His-Asp-His-Gly peptide obtained *in silico* (black and red) and in NMR experiments (blue and orange).

© MPI-NAT, P. Dobrev

Simulation at constant pH

The downloadable movie is a 5 ns constant-pH MD simulation (pH=4) of the turkey ovomucoid third domain in water. The acidic amino acids Asp and Glu are drawn with sticks. They appear in red colour as negatively charged (deprotonated) and in blue colour as positively charged (protonated) residues, respectively. The proton is illustrated as a ball.

Constant pH MD simulation of turkey ovomucoid third domain in water

MPEG-1 Movie File (15 MB)

Constant pH MD simulation of turkey ovomucoid third domain in water

MOV Video File (873 KB)

Average protonation state of the acidic amino acids of turkey ovomucoid third domain

This animation shows the average protonation state (blue=protonated, red=deprotonated) of the acidic amino acids of turkey ovomucoid third domain at different pH values. The plot shows the extent of deprotonation as a function of pH: the titration curve of the protein. The higher the affinity of the protein for the protons, the more the titration curve is shifted to the right. From the titration curve, the apparent pK_a values of the amino acids are obtained.

Publications

Dobrev, P.; Vemulapalli, S. P. B.; Nath, N.; Griesinger, C.; Grubmüller, H.

Probing the Accuracy of Explicit Solvent Constant pH Molecular Dynamics Simulations for Peptides

J. Chem. Theory Comput. 2020, 16, 4, 2561–2569

Source

DOI

Dobrev, P.; Donnini, S.; Groenhof, G.; Grubmüller, H.: Accurate three states model for amino acids with two chemically coupled titrating sites in explicit solvent atomistic constant pH simulations and pK_a calculations. Journal of Chemical Theory and Computation 13 (1), pp. 147 - 160 (2017)

MPG.PuRe

DOI

publisher-version

supplementary-material

Donnini, S.; Ullmann, T.; Groenhof, G.; Grubmüller, H.: Charge-neutral constant pH molecular dynamics simulations using a parsimonious proton buffer. Journal of Chemical Theory and Computation 12 (3), pp. 1040 - 1051 (2016)

MPG.PuRe

DOI

publisher-version

Bennett, W. F. D.; Chen, A. W.; Donnini, S.; Groenhof, G.; Tieleman, D. P.: Constant pH simulations with the coarse-grained MARTINI model—Application to oleic acid aggregates. Canadian Journal of Chemistry 91 (9), pp. 839 - 846 (2013)

MPG.PuRe

DOI

publisher-version

Donnini, S.; Tegeler, F.; Groenhof, G.; Grubmüller, H.: Constant pH molecular dynamics in explicit solvent with lambda-dynamics. Journal of Chemical Theory and Computation 7 (6), pp. 1962 - 1978 (2011)

MPG.PuRe

publisher-version

Usage

This website provides usage instructions for our "in house" version of Gromacs 3.3.1 and Gromacs 3.3.3 for performing constant pH MD as described in the publications by Donnini et al. (2011) and Dobrev et al. (2017). [more]