Mathematical bioPhysics
The group pursues a mathematical physics-approach to study phenomena in biophysics.
Our main research focus is the non-equilibrium statistical mechanics of single molecules/particles and the collective behavior of larger molecular and up to sub-cellular assemblies. In particular, we aim at a trajectory-based description of macromolecular conformation dynamics as well as of their spatial transport, binding, and reactions. From a fundamental perspective we are focusing on relaxation phenomena of Markovian and non-Markovian observables from far-from-equilibrium quenches as well as the generic physical origin and understanding of broken time-translation invariance. In the analysis of stochastic many-body systems we aim at an understanding of emerging collective effects from a trajectory perspective. In our work we employ rigorous analysis corroborated by computer simulations. Please see Recent research activities below for more details
Recent research highlights
Time irreversibility in systems observed at coarse resolution
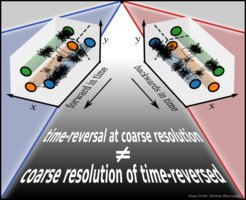
A broken time-reversal symmetry is central to non-equilibrium physics and a prerequisite for life. However, it turns out to be quite challenging to unambiguously define and quantify time-reversal symmetry (and violations thereof) in practice, that is, from observations. Measurements on complex systems have a finite resolution and generally probe low-dimensional projections of the underlying dynamics, which are well known to introduce memory. In situations where many microscopic states become “lumped” onto the same observable “state” or when introducing “reaction coordinates” to reduce the dimensionality of data, signatures of a broken time-reversal symmetry in the microscopic dynamics become distorted or masked. In this recent Perspective article, we highlight why, in defining and discussing time-reversal symmetry and quantifying its violations, the precise underlying assumptions on the microscopic dynamics, the coarse graining, and further reductions are not a technical detail. These assumptions decide whether the conclusions that are drawn are physically sound or inconsistent. We summarize recent findings in the field and reflect upon key challenges.
Thermodynamic Bounds on Generalized Transport
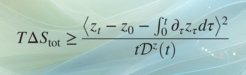
We prove that the transport of any differentiable scalar observable in d-dimensional nonequilibrium systems is bounded from above by the total entropy production scaled by the amount the observation “stretches” microscopic coordinates. The result—a time-integrated generalized speed limit—reflects the thermodynamic cost of transport of observables, and places underdamped and overdamped stochastic dynamics on equal footing with deterministic motion. Our work allows for stochastic thermodynamics to make contact with bulk experiments, and fills an important gap in thermodynamic inference, since microscopic dynamics is, at least for short times, underdamped. Requiring only averages but not sample-to-sample fluctuations, the proven transport bound is practical and applicable not only to single-molecule but also bulk experiments where only averages are observed, which we demonstrate by examples. Our results may facilitate thermodynamic inference on molecular machines without an obvious directionality from bulk observations of transients probed, e.g., in time-resolved x-ray scattering.
Mathematics of deception in asset-exchange models
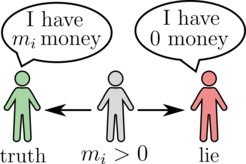
While the exponential Boltzmann distribution usually applies to the microscopic "thermalized" world, it coincidentally also happens to be a good description of the wealth statistics in real-world economies. The origin of such Boltzmann-like wealth distributions can be understood within a simple stochastic model that considers a population of agents exchanging money at random: any two agents can exchange one unit of money based on the outcome of a coin flip. However, because agents cannot incur debts, the transaction becomes unidirectional when one agent is broke, allowing only that agent to gain money. This results in an exponential wealth distribution, which indeed agrees with the bulk of empirically obtained wealth distributions in many economies.
But what happens when some agents cheat and falsely claim they are bankrupt? In such scenarios, the cheating agent always gains money irrespective of their actual wealth. This study demonstrates how the presence of such cheaters can be inferred from the overall wealth distribution, allowing an external observer to detect hidden cheaters by simply looking at the variance of the distribution. Furthermore, it is shown that cheating does not always yield immediate benefits. In fact, when the number of cheaters is small compared to the honest agents, there exist a finite cheating probability at which the money owned by the cheaters undergoes a second order discontinuity.
Increasing ignorance may benefit thermodynamic inference
Molecular machines operate far from equilibrium, dissipating energy and increasing the entropy of their surroundings. The irreversibility of their motion, even with the unprecedented spatiotemporal resolution of recent single-molecule studies, is blurred by thermal fluctuations and the fact that experiments typically observe only a coarse projection of microscopic dynamics. This makes the inference of broken time-reversal symmetry a daunting task. We describe how to systematically improve entropy-production estimates from observed coarse trajectories using a method called "milestoning". With milestoning, we coarse grain trajectories to a (generally non-Markovian) jump process on a network of "milestones" that do not cover the entire configuration space. Thereby we effectively increasing our ignorance of the underlyng configuration space and yet concurrently render the resulting dynamics "closer to" the unobservable microscopic dynamics, by eliminating trivial recurrences on faster timescales. We present diverse examples where milestoning systematically improves thermodynamic inference assuming a given range of memory.
Heating and cooling are fundamentally asymmetric

Using an optically trapped colloidal particle, we show, in collaboration with the group of Raul Rica (Univ. de Granada) that microscale systems quenched far from thermodynamic equilibrium heat up faster than they cool down. We show, by experiment and by mathematical proofs, that between any pair of temperatures, heating is not only faster than cooling but the respective processes in fact evolve along fundamentally distinct pathways, which we explain with a new theoretical framework that we coin “thermal kinematics”. Our results change the view of thermalization at the microscale are expected to have a strong impact on energy-conversion applications and thermal management of microscopic devices such as Brownian heat engines.
Some certainty about the uncertainty of kinetic inference

A notorious problem in inference is the uncertainty of estimates in the presence of limited or insufficient sampling. In the worst case scenario, large uncertainties are known to lead to erroneous conclusions. What is worse, so far it was not possible to make any reliable (unbiased) statements about the uncertainty of the estimates without substantial knowledge or intuition of the observed process, which is typically not available. By developing a new mathematical framework to control uncertainty of inferred rates and even their expected range of values in arbitrarily small samples, we provide certainty about the uncertainty of kinetic inference without any prior knowledge about the underlying dynamics. This finally opens the door to rigorous control and unbiased estimation of errors in the presence of limited sampling.
Direct route to thermodynamic uncertainty relations and their saturations
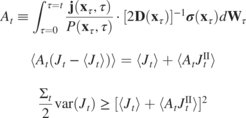
Thermodynamic uncertainty relations (TURs) bound the dissipation in nonequilibrium systems from below by fluctuations of any observed current. TURs have been developed in various flavors, depending on the physical setting. In contrast to elaborate techniques employed in derivations of respective TURs, we prove these TURs directly from the Langevin equation using stochastic calculus. This establishes the TUR as an inherent property of stochastic equations of motion, akin to quantum-mechanical uncertainty. By including correlations, we further derive a new, sharpest TUR for transients. Our simplest and most direct proof unifies TURs and determines conditions under which they saturate, thus enabling a more accurate thermodynamic inference.
Thermodynamically consistent phase-field theory including nearest-neighbor pair correlations
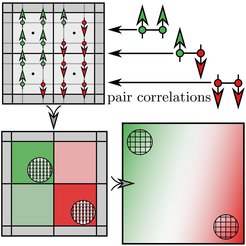
Our current understanding of interracial phenomena and phase separation is mostly still based on ideas that disregard correlations between particles. In our work we illuminate unexpected effects of correlations on the structure and thermodynamics of interfaces and in turn phase separation, which are decisive in systems with strong interactions. We directly evaluate the continuum limit of the Ising model on the Bethe-Guggenheim level to derive a Cahn-Hilliard free energy that takes into account pair correlations. For a one-dimensional interface in a strip geometry, these give rise to an effective interface broadening at interaction strengths near and above the thermal energy, which is verified in the full Ising model. Interface broadening is the result of an entropy-driven interface delocalization, which is not accounted for in the widely adopted mean field theory. Pair correlations are required for thermodynamic consistency as they enforce a thermodynamically optimal local configuration of defects and profoundly affect nucleation and spinodal decomposition at strong coupling.
Threefold necessity for coarse graining in time-average statistical mechanics
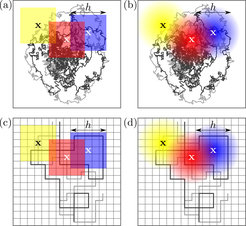
It is well known that all experiments interrogating individual molecules and particles are limited by a finite precision and finite statistics. Yet, existing theoretical approaches for estimating the probability density of a particle’s location and current from individual trajectories failed to account for that. Within the newly developed theoretical framework we explain why accounting for a finite resolution and statistical sampling is not only necessary for well defined mathematical and statistical properties, but is also beneficial for the inference of thermodynamic and kinetic properties in small systems arbitrarily far from thermodynamic equilibrium.
The work was published in a joint publication in Physical Review Letters and Physical Review Research.
Scattering fingerprints of two-state dynamics
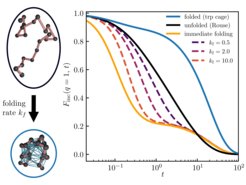
Particle transport in complex environments such as the interior of living cells is often non-Fickian or anomalous, that is, it deviates from the laws of Brownian motion. Such anomalies may be the result of small-scale spatio-temporal heterogeneities in, or viscoelastic properties of, the medium, molecular crowding, etc. Often the observed dynamics displays multi-state characteristics—distinct modes of transport dynamically interconverting between each other in a stochastic manner. Reliably distinguishing between single- and multi-state dynamics is challenging and requires a combination of distinct approaches. To complement the existing methods relying on the analysis of the particle’s mean squared displacement, position- or displacement-autocorrelation function, and propagators, we developed a theoretical framework for two-state scattering signatures—the intermediate scattering function and dynamic structure factor—and applied it to the analysis of simple model systems as well as particle-tracking experiments in living cells. We considered inert tracer-particle motion as well as systems with an internal structure and dynamics. Our results may generally be relevant for the interpretation of state-of-the-art differential dynamic microscopy experiments on complex particulate systems, as well as inelastic or quasielastic neutron (incl. spin-echo) and x-ray scattering probing structural and dynamical properties of macromolecules, when the underlying dynamics displays two-state transport.
Colloids dancing on a fractal carpet made of light
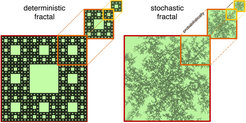
Particle dynamics frequently occur in complex environments; in technology, e.g. atoms moving on structured surfaces, as well as in nature, e.g. transcription factors moving in the cell’s nucleus. These dynamics have often been modeled assuming that the medium resembles a fractal. Fractals are idealized geometrical objects that appear identical on all length scales (see Figure). Whether fractal concepts can actually be applied, has been scrutinized in the present study. In collaboration with the group of Stefan Egelhaaf (Univ. of Düsseldorf) we used a model system consisting of colloidal particles moving in a laser speckle pattern to tie experimental observations reliably to a fractal structure whose fractal dimension we were able to tune. The agreement between experimental observations and theoretical predictions reveals that the particles explore the speckle in a self-similar, fractal manner at least over four decades in time and on length scales up to 20 times the particle radius. Our work establishes the requirements that are necessary for fractal diffusion to be applicable, and provides methods to extract the fractal dimension. The importance of a fractal medium is discussed in the context of gene regulation.
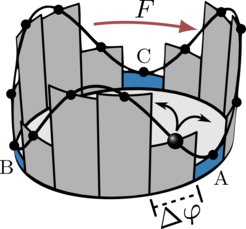
Emergent memory and kinetic hysteresis in strongly driven networks
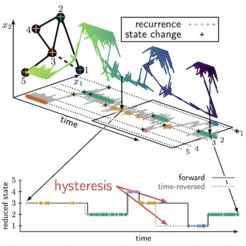
In elastic materials, friction is known to cause a phenomenon called hysteresis – more energy is required to stretch a rubber band than is released during unloading. As a result, the rubber band becomes warm. On microscopic scales where thermal fluctuations are important, such as in molecular motors operating far from equilibrium, hysteresis emerges in the form of a broken time-reversal symmetry. In our paper we report on a novel form of hysteresis that is of a purely kinetic nature and emerges as soon as a system does not locally equilibrate in metastable states. This gives rise to memory in the observed dynamics; that is, state changes depend on past states.
Kinetic hysteresis arises from the finite duration of transition paths, which are completed transitions between pairs of metastable states. We derive, for the first time, a network theory that preserves the microscopic dissipation and accounts for the finite duration of transition paths. We unravel three ingrained symmetries of the dynamics that determine the characteristics of the observed memory. These symmetries reveal hidden, vital information about the dynamics even in the limit where the hysteresis may become negligibly small. We use the theory to explain the counterintuitive “catch-bond” phenomenon, where a larger mechanical load prolongs the lifetime of an adhesion bond.
Our results pave the way toward a deeper understanding of violations of time-reversal symmetry in the presence of memory. In practice, the symmetries unraveled in our work allow for robustly detecting the coexistence of multiple transition pathways in a measured time series without resolving them individually.
Criticality in cell adhesion
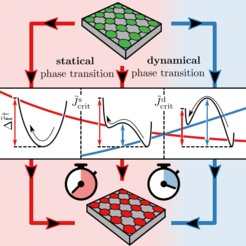
Cells, the fundamental building blocks of living organisms, stick to other cells via a process called cell adhesion. For multicellular organisms cell adhesion plays a crucial role in the immune response, wound healing, and cancer development. Cell adhesion is mediated by so-called adhesion bonds. The breaking and formation of individual adhesion bonds is coupled via thermal fluctuations of the anchoring cell membrane. The last two decades of experiments and theory have shown that cell adhesion may in fact be accurately described by a model originally developed to describe ferromagnetism: the Ising model.
In our work we generalize the Ising model in order to explain how membrane fluctuations and external forces on the cell induce many-body effects, and how these in turn affect the equilibrium behavior and dynamical properties of cell adhesion. Strikingly, changes in the membrane rigidity can prolong or shorten the mean time a cell adheres to a stiff substrate, which in the thermodynamic limit of many adhesion bonds leads to the notion of a novel kind of dynamical critical point. The existence of a dynamical critical point is equivalently implied in the context of magnetization reversal times in ferromagnetic materials.
Thermodynamic limits to anomalous diffusion
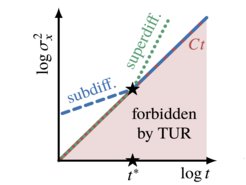
Thermal, Brownian fluctuations in physical systems were found to be bounded by a universal physical relation called the "thermodynamic uncertainty relation". Concurrently, experiments tracking individual particles or molecules frequently show fluctuations that deviate strongly from the Gaussian laws of Brownian motion – a phenomenon commonly referred to as "anomalous diffusion".
In our work we show, for the first time, that the two seemingly disjoint if not orthogonal fields of research – stochastic thermodynamics and anomalous diffusion – may be fruitfully combined to derive a new universal physical bound on the experimentally often unknown temporal extent of anomalous diffusion.
The paper was covered in a Viewpoint in Physics: https://physics.aps.org/articles/v14/116
Introducing: Time-average statistical mechanics
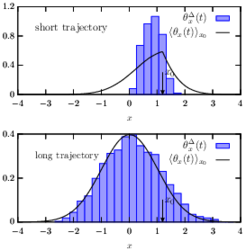
Many experiments on soft and biological matter probe individual trajectories. It is typically not feasible to repeat these experiments sufficiently many times in to apply the traditional concepts of (ensemble) statistical mechanics. It is, however, straightforward to analyze such data by means of time-averaging along individual realizations. However, a correct rationalization and interpretation of such time-averaged results requires the framework of “time-average statistical mechanics”.
In our work we develop a spectral-theoretic approach to describe fluctuations of time-average observables evolving from general (incl. non-equilibrium) initial conditions, and consider both, reversible and irreversible (i.e. driven) dynamics. Our results are directly applicable to a diverse range of phenomena underpinned by time-average observables in physical, chemical, biological systems, such as single-particle tracking and single-molecule spectroscopy, and may also find important applications in econophysics.
An unforeseen asymmetry in relaxation to equilibrium: Nanoscale warming is faster than cooling
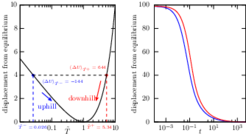
According to elementary physics cooling and warming rates should be identical if conditions are the same. A thermodynamic system generally evolves, or “relaxes,” to minimize its free energy, and if the total free energy difference between the initial and final conditions is the same in both cases, warming and cooling should be equally fast. As a result of a subtle imbalance in how the probability distribution of any system evolves under conditions of warming or cooling we find, however, that relaxation happens faster “uphill” than “downhill”.
We prove that near stable minima and for all quadratic energy landscapes it is a general phenomenon that also exists in a class of non-Markovian observables probed in single-molecule and particle-tracking experiments. The asymmetry is a general feature of reversible overdamped diffusive systems with smooth single-well potentials and occurs in multiwell landscapes when quenches disturb predominantly intrawell equilibria. Our findings may be relevant for the optimization of stochastic heat engines.
The paper was covered in Physics Focus: https://physics.aps.org/articles/v13/144















