Generalized Correlation for Biomolecular Dynamics
Oliver F. Lange and Helmut Grubmüller
Generalized versus Pearson correlation coefficients
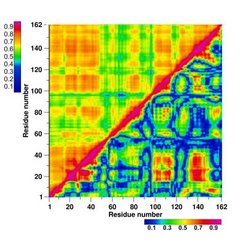
Correlated motions in biomolecules, in particular proteins, are ubiquitous and often essential for biomolecular function. Correct assessment of correlated motions, both experimentally and from theory and simulations, is therefore crucial for a quantitative understanding of biomolecular function. The accurate characterization of correlated motions would also improve the interpretation of NMR experiments and X-ray diffusive scattering data. Here we describe how to obtain correlations from MD simulations. Any experiment which probes correlations in the motion of pairs of atoms would do so in a way which is invariant to the definition of the Cartesian coordinate system. Therefore, we need to obtain a measure, which is also invariant to the chosen coordinate system.
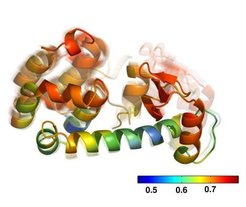
Correlated motion of domains
Pearson correlation measure
The first trial, which generalized the Pearson correlation coefficient, rests on calculation of the normalized covariance matrix of atomic fluctuations,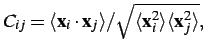
where
and
are the positional fluctuation vectors of atoms 
and 
, respectively, in the molecular fixed frame. This established approach, however, misses a considerable fraction of the correlated motions and, therefore, usually underestimates atomic correlations [Lange, 2006]. This limitation is mainly due to three assumptions:
- First, estimates of correlations from the Pearson coefficient are only strictly valid if 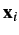and 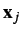are co-linear vectors.
- Second, a linear approximation. Thus, the Pearson correlation coefficient misses non-linear correlations.
- Third, the measure is not well-defined, because it is not invariant to rescaling.
Generalized Correlation in a simple picture
Generalized correlation
- any correlation is captured
- sound information theoretical basis
- scaling invariant
- can consistently be used for measuring correlation between groups of atoms of any size
- linearized version exists, and allows to separate purely non-linear from linear correlations
The generalized correlation measure rests on the fundamental definition of independence of random variables. Accordingly, two random variables are independent, if and only if their joint distribution is a product of their marginal distributions,
.
The basic idea is to quantify the correlation between variables X, Y as the deviation between both sides of the above equation, i.e., by the deviation from the case of two independent random variables (see figure). This is done by mutual information, as laid out in [Lange, 2006].
Software
We have implemented the tool g_correlation for the GROMACS framework, which allows the calculation of both linear and non-linear generalised correlation coefficients. You will need to install GROMACS if you have not already done so, please read the INSTALL instructions. Note that g_correlation also works with .xtc files created by newer versions of GROMACS. In the subdirectory mfiles you will find some scripts for MATLAB. read_blitz.m allows you to read the *.dat output of g_correlation. This will give you a matrix of the correlation coefficients in MATLAB. To plot a matrix as shown above, you can use plot_corr_matrix.m. If you have any questions on the installation process, feel free to send a mail.
Changelog:
- Ver 1.x: C-version
- Ver 1.0.1: added Makefile_gmx321 to allow simple installation together with gromacs 3.2.1
- Ver 1.0.2: removed problem with MPI due to deprecated #define statement (MPI job exits with signal 11)
- Ver 1.0.3: g_correlation -f now also properly reads .gro input files on top of .tpr and .pdb
The software is free for everyone. However, if you use it for publications or presentations you should cite the original publication [Lange, 2006]. The current version applies an algorithm from [4], which should be cited, too. Please note that the software is distributed with NO WARRANTY OF ANY KIND. The author is not responsible for any losses or damages suffered directly or indirectly from the use of the software. Use it at your own risk. Enjoy!
Download
Publication