Per|Mut
Spatially resolved hydration entropies from atomistic simulations
The statistical mechanics of the first few hydration layers is vital for many biophysical processes, such as protein folding and unfolding, protein function, lipid bilayer self-assembly, and ligand binding. These processes are governed by a fine-tuned free energy balance of competing enthalpy and entropy contributions. Despite extensive experimental and theoretical efforts, the molecular mechanisms of solvent-related free energy contributions are often elusive, especially at topologically and chemically heterogeneous surfaces like proteins or lipid bilayers. To better understand, e.g., the effects of individual amino acids on the solvent-related free energy contributions, a spatial resolution of both solvent enthalpy and entropy is necessary. Whereas the enthalpy component can be readily calculated from a molecular dynamics force field, sampling the configuration space in order to converge entropy contribution presents a significant challenge. First, the permutation symmetry of the N identical water molecules results in a combinatorial explosion and N! physically configurational subspaces. Secondly, the extremely high dimensionality of the configuration space causes sampling problems due to the “curse of dimensionality”.
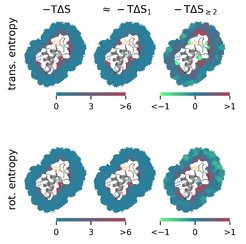
To overcome these two problems, we developed the new method Per|Mut, to calculate spatially resolved solvent entropies from atomistic simulations. The method uses a permutation reduction (implemented in the program g_permute) to increase sampling by the Gibbs factor N! without changing the physics. In addition, Per|Mut employs a third-order mutual information expansion to decompose the solvent entropy into physically interpretable contributions from individual molecules as well as from two- and three-body correlations. The method yielded accurate entropies for test systems with argon and solvated alkanes. When applied to the solvation statistical mechanics of hydrated octanol and the protein crambin, the method revealed the local effects of individual chemical groups or side chains on the solvent entropy.
g_permute
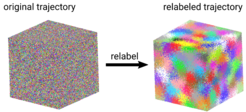
In permutation reduction, the trajectory is mapped into a configurational subspace by exploiting the permutation symmetry of the N identical molecules, in order to recover the Gibbs factor. Accordingly, for each frame of a molecular dynamics trajectory, our software g_permute relabels the solvent molecules, such that the resulting configuration space volume is reduced by a factor of N!. The combinatorial explosion of a naive implementation is here overcome by transforming the task into a linear assignment problem, for which algorithms with complexity O(N^3) exist.

