Variational Morphing: Determining Free Energy Differences Through Optimal Non-Linear Lambda States
Free energy calculations based on atomistic Hamiltonians and sampling are key to a first principles understanding of biomolecular processes, material properties, and macromolecular chemistry. Here, we generalize the Free Energy Perturbation method and derive non-linear Hamiltonian transformation sequences for optimal sampling accuracy that differ markedly from established linear transformations. We show that our sequences are also optimal for the Bennett Acceptance Ratio (BAR) method, and our unifying framework generalizes BAR to small sampling sizes and non-Gaussian error distributions. Simulations on a Lennard-Jones gas show that an order of magnitude less sampling is required compared to established methods.
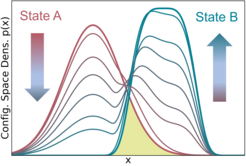
Gradients in free energies are the driving forces of physical and biochemical systems and enable quantitative descriptions of e.g. molecular recognition processes, drug binding, transmembrane transport, or functional conformational motions of proteins or complexes. To predict free energy differences computationally with high accuracy, Molecular Dynamics based state of the art methods use ‘alchemical transformations’, where sampling is not only conducted in the two final states of interest (e.g. two ligand types binding to a common receptor), but also in intermediate states. These are defined along a morphing path - typically a linear interpolation of the Hamiltonians (i.e. the total interaction energies) of the start and the end state. The term ‘alchemical’ refers to the fact that differing atoms are transformed from one type into another along the morphing path. Even though interpolated atom types do not exist in reality, the information gained from sampling in these intermediate states drastically improves the accuracy of the final free energy estimates.
However, linear transformations are still a very special case amongst all possible transformations. In this project, we therefore also considered non-linear transformations and analytically derived the intermediate states yielding the optimal accuracy free energy estimates. These states differ markedly from established linear transformations. An order of magnitude improvement in the amount of required sampling, and therefore, simulation time, was obtained for a test system with Lennard-Jones interactions.
